Typical Kotlin

This post was originally posted on KotlinDevelopment.com, which is now unavailable.

Let me invite you on a tour of Kotlin’s type system, exploring how some of the language constructs we take for granted in our everyday use - as they just “make sense” - work.

Disclaimer: Some illustrations presented here to explain the type hierarchy are inspired by the ones in this blog post by Nat Pryce from 2 years ago, as well as in KotlinConf 2017 talks by both Svetlana Ivanova and Christina Lee.

What’s a type?

First things first, what exactly is a type? Types are what let us and the compiler define expectations we have for any given object. What properties and methods can be called on it, where it can be passed as a parameter, where it can be assigned.

Every variable, property, parameter, and expression has a type in Kotlin at compile time - this static typing is what guarantees that, for example, no calls are made to non-existent functions. This eliminates a whole class of possible runtime errors that might occur in dynamically typed languages.

It’s important to note that types are not equivalent to classes. We are creating a new type every time we declare a class, interface, object, or typealias (going forward, we’ll stick to just classes for simplicity). In fact, in all of these cases, we’re creating multiple new types with these declarations. Let’s take just the case of a boring, empty class:

class Hello

By defining this class, we’ve already created the Hello and Hello? types. These are separate and very different types, as the compiler forces us to explicitly handle the possible nullability of a Hello? in the form of null checks, while letting us use a Hello relatively freely in comparison, since it knows it’s safe to do so.

Creating a class with a type parameter introduces yet more types:

class List<T>

In fact, this unbounded T type parameter introduces infinitely many types. Some of these would be List<String>, List<String>?, List<String?>, List<String?>?, List<List<Int>>, List<in String>, List<*>… Just to mention a few.

The Any type

Just like classes, types exist in a hierarchy. We’ll put aside nullable types for a moment, and look at just the hierarchy of non-nullable types. This looks essentially the same as the hierarchy formed by the respective classes that define these types.

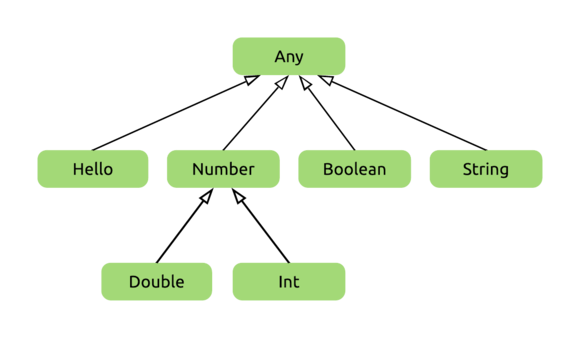
The root of Kotlin’s type hierarchy is the Any type (just like the Any class is the root of the class hierarchy). This type defines basic functions such as equals, hashCode, and toString, which are available on all object instances in Kotlin, as they all have Any as their supertype.

Supertype: Y having a supertype of X means that an object of type Y can be used in any place an X is expected, and it will behave as an X is expected to behave. (This is what the Liskov substitution principle, one of the SOLID principles states.)

Classes with no explicit superclass inherit directly from the Any class, and therefore the (non-nullable) types produced by these classes are direct subtypes of the Any type. An example of this is the Hello class we’ve defined earlier. As Kotlin doesn’t distinguish between primitives and wrappers, the primitive types (Int, Double, Boolean) are also subtypes of Any.

Subtype: the opposite of a supertype. Y is a subtype of X if and only if X is a supertype of Y.

(The number types aren’t direct subtypes of Any, but instead they are subtypes of Number, which defines some of the common functionality of numerical types.)

The parallel nullable and non-nullable type hierarchies

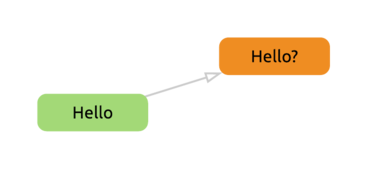
Now, let’s get to how nullable types come into the picture. The relation of a given type and it’s counterpart is fairly simple to determine. The non-nullable type is a more concrete type, as it can only accept a subset of the values that the nullable type can.

Applying this to every type in our type hierarchy, we get two parallel hierarchies, which we can visualize like so:

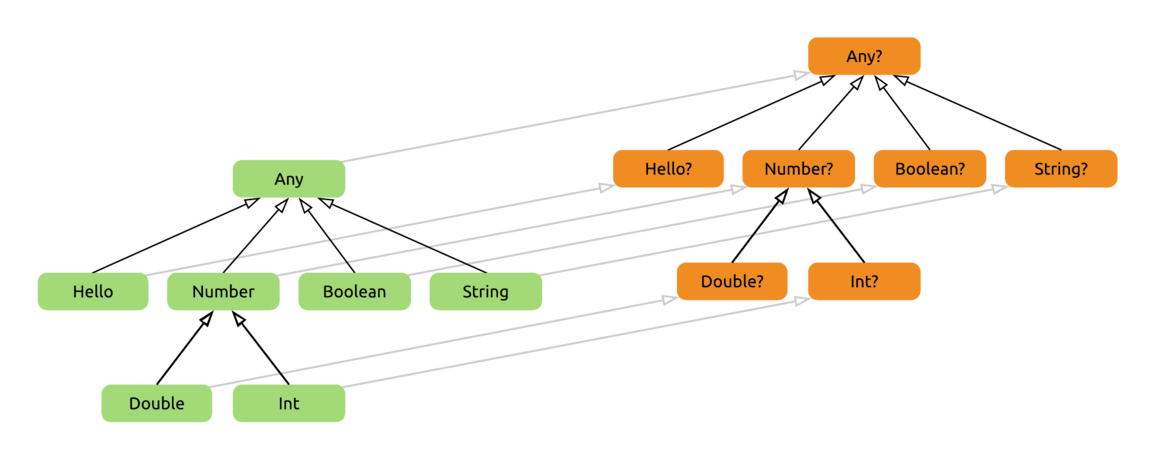
Looking at this, we can see that the real root of the entire type hierarchy is the Any? type. This means that a variable of type Any? is able to store any arbitrary object.

We can check if all the indirect relations between types also make sense. As an example, we see that Double is a subtype of Number?, according to the diagram. This does in fact makes sense, since a Double really does produce all the behaviour that is expected from a Number?. We can also intuitively feel that an object of type Double can be safely stored in a variable of type Number?.

The Elvis operator

The Elvis operator is most often used to handle cases where a value is null and we have to use a substitute value in its place. You probably know how it works - if its left hand side is null, it will simply return the right hand side. What about the return type of the entire expression though?

Most often, we use the Elvis operator to provide a non-nullable value that has the same type as the left hand side:

val maybeString: String? = null
val definitelyString = maybeString ?: "replacement"

This is the straightforward case, definitelyString will simply have the type String inferred here, as we’re expecting it.

But how does the compiler choose the correct type? What if we use different types on the two sides of the operator, and not just the nullable and non-nullable variant of the same type?

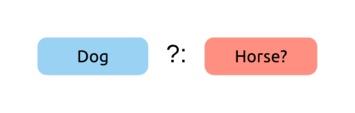
Let’s answer these questions by looking at some examples. Here’s the hierarchy we’ll be using for these, it’s pretty straightforward:

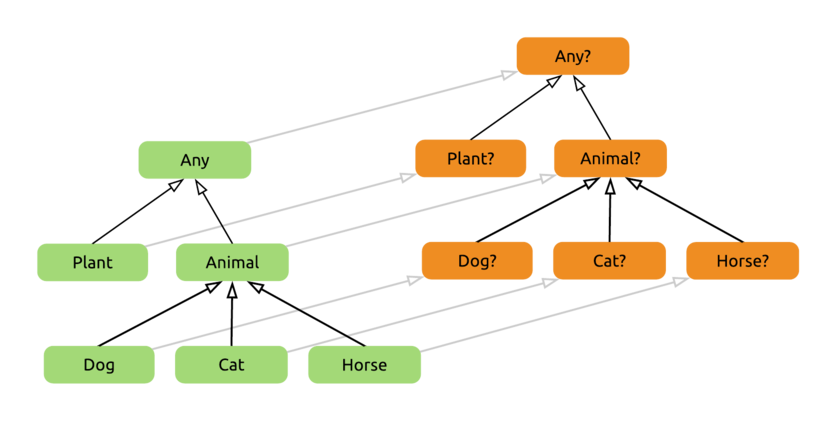
Both nullable

Let’s evaluate an Elvis expression between a Dog? and a Horse? type. I’ll be using this notation to describe this task:

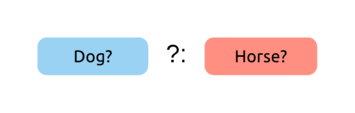
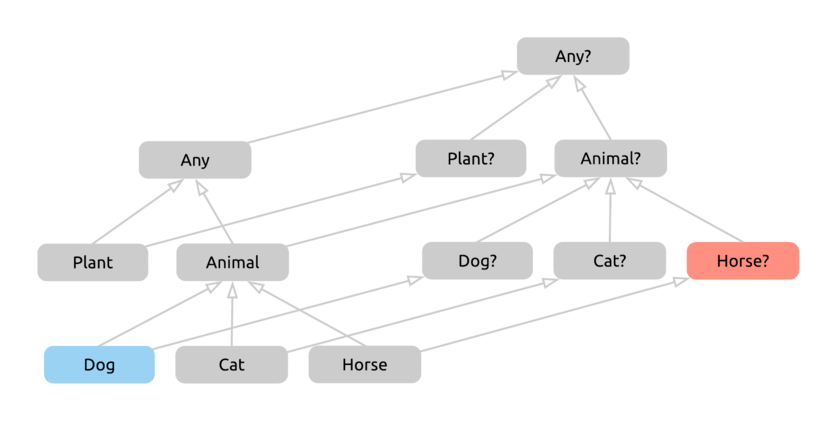
First, we find these types in the hierarchy:

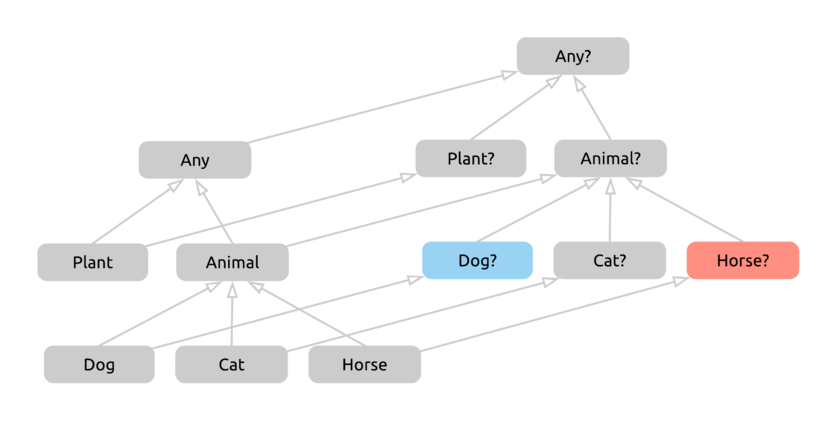
Now we have to figure out what type the Elvis expression above will return. As our first guess, let’s take the first common supertype of these two sides and see if that works.

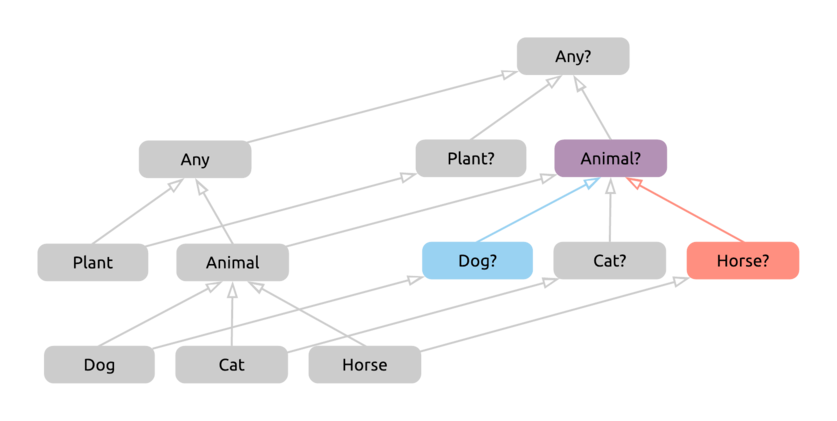
We got Animal? as our type for the entire expression created by the Elvis operator. This seems fine. We’ll either have a Dog or a Horse, plus they might be null, and an Animal? can hold either of these possible values - and we can check one by one that no other, more concrete type can do so. If we verify our result - for example, in IntelliJ with type inference - we’ll see that we have indeed found the correct return type.

Right nullable

Here’s our next example to evaluate - we’ve changed the left hand side to a non-nullable type.

We can find these types quickly now:

Again, we’ll take the first common supertype, as this worked well for us before, and we have no reason to doubt it. We could take multiple routes from Dog to Animal? here, however, this doesn’t affect the end result.

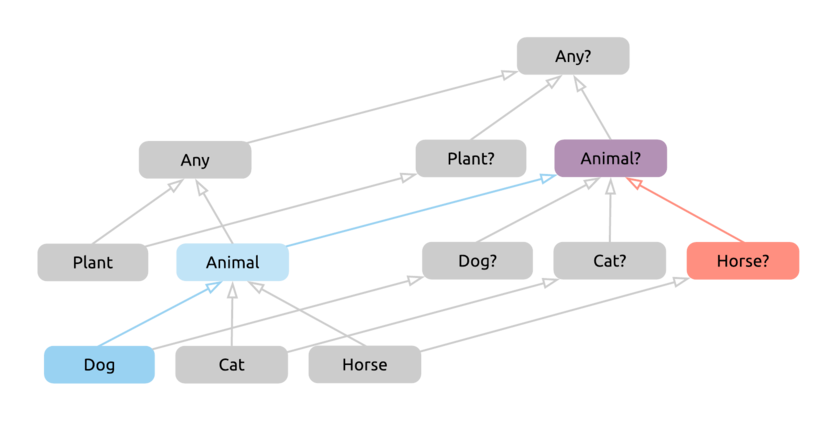
We have a few more jumps now, but the result seems sensible. If we check in IntelliJ, we are again correct as far as the return type of an expression like this goes. If we take a step back however, we’ll also find that the Elvis operator is simply redundant in this case - the left side can never be null. Nevertheless, if we were to still write this down and not heed the IDE’s warnings, we’d get Animal? as its return type.

Left nullable

As a non-nullable type on the left side makes no sense, we’ll get to our last combination of nullabilities for the two sides:

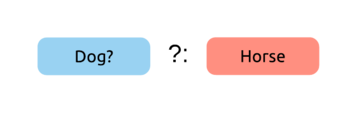
We identify the types in the hierarchy:

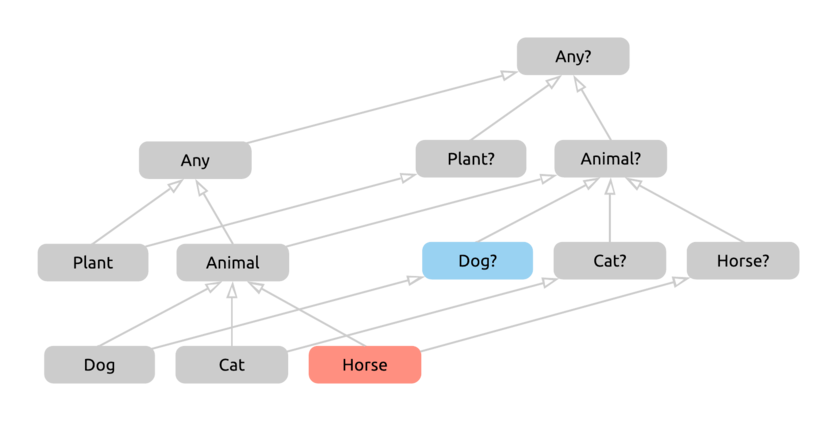
And we take the first common supertype of these two. Again, we could take multiple routes from Horse to Animal?, but it is the first common supertype.

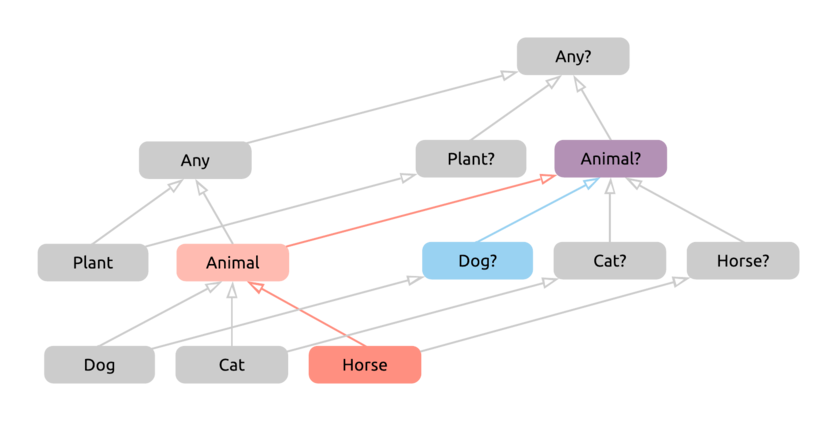
Something has gone wrong here, however. If we take a moment to think, we’ll find the nullable result of Animal? to be overly cautious. If the left hand side of the expression happens to be null, we’ll be using the right side instead, which will give us a non-nullable Horse value. If the left side is not null, we get a non-nullable Dog as the result.

This means that Animal would be a perfectly reasonable result for the expression as well. What went wrong, how did we get a nullable type when none is needed? Our mistake was to treat the left side as nullable, even though the expression will enver return null from that side.

To fix this, we’ll take the non-nullable version of the type on the left, and the type as it is on the right, and we find the first common supertype of these two types.

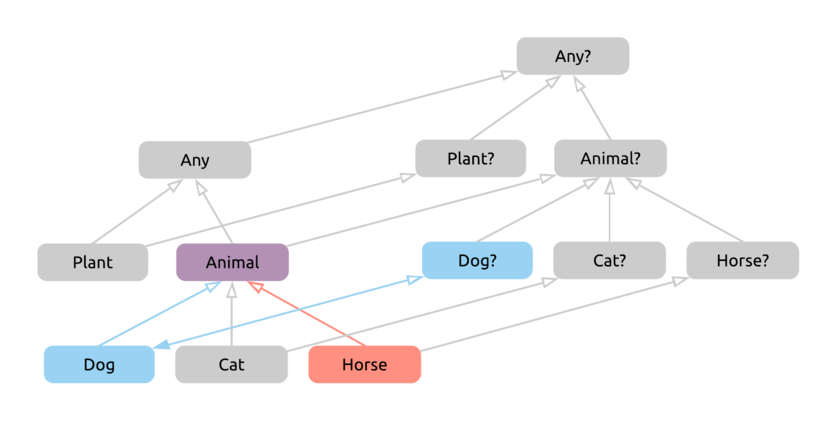
In our case, this means first taking Dog? back to the non-nullable side of the hierarchy to Dog, and then finding the first common supertype with Horse, which, as expected, will now be the correct Animal type.

The Unit type

Unit is a special type in Kotlin. The documentation describes it as the type with only one value. As far as its code goes, this is achieved simply by declaring Unit as a singleton object. Here’s its entire source:

public object Unit {
    override fun toString() = "kotlin.Unit"
}

This of course wouldn’t be enough for Unit to do all the things it does, there’s also a bit of special treatment by the compiler involved to achieve these.

The most important of these is that functions that return no meaningful value return Unit instead in Kotlin. This is a meaningless return value (as it’s an empty object), but this way, all functions work semantically the same way: they all return something. In comparison, Java has to give special treatment to void returning functions - for example, we can’t assign their return type to a variable.

Unit being a proper type also comes in handy with generics - if we have a Task<T> type and we need an instance that returns no result when it’s done, in Java we’d have to use yet another new type, Void, which is a completely separate thing from the void keyword. In Kotlin, we can use the same Unit everywhere to describe the lack of meaningful data.

The Nothing and Nothing? types

A value that never exists

Nothing can be quite similar to Unit on first glance. Nothing is a class that can never be instantiated. Again, this is backed by its very short source:

public class Nothing private constructor()

This in itself leads to some interesting consequences for using Nothing. For example, if a function has Nothing as its return type, we know that it can never return, since it has no way of acquiring the instance of Nothing it would return. This, again, is different from Unit returning functions - those did return something, that value just wasn’t meaningful.

What does a function that never returns look like? It might contain an infinite loop, or it might always throw an exception instead of terminating normally:

fun loopy(): Nothing {
    while (true) {
        println("Loop!")
    }
}

fun exceptional(): Nothing {
    throw IllegalStateException()
}

The Kotlin compiler allows both of these functions to compile since it understands control flow and sees that neither will ever reach a return statement. Of course, both of these could just return Unit, but this way, we can signal to client code that they will never return.

Why would we want to do this? For example, because the IDE can now warn callers about code that’s placed after a call to these Nothing-returning functions, which will never be executed:

Nothing as a bottom type

The Nothing type gets some additional special treatment from the compiler. Since it can never exist, it can serve in the type system as a bottom type.

Bottom type: in subtyping systems, the bottom type is the subtype of all types.

This updates our hierarchy like so:

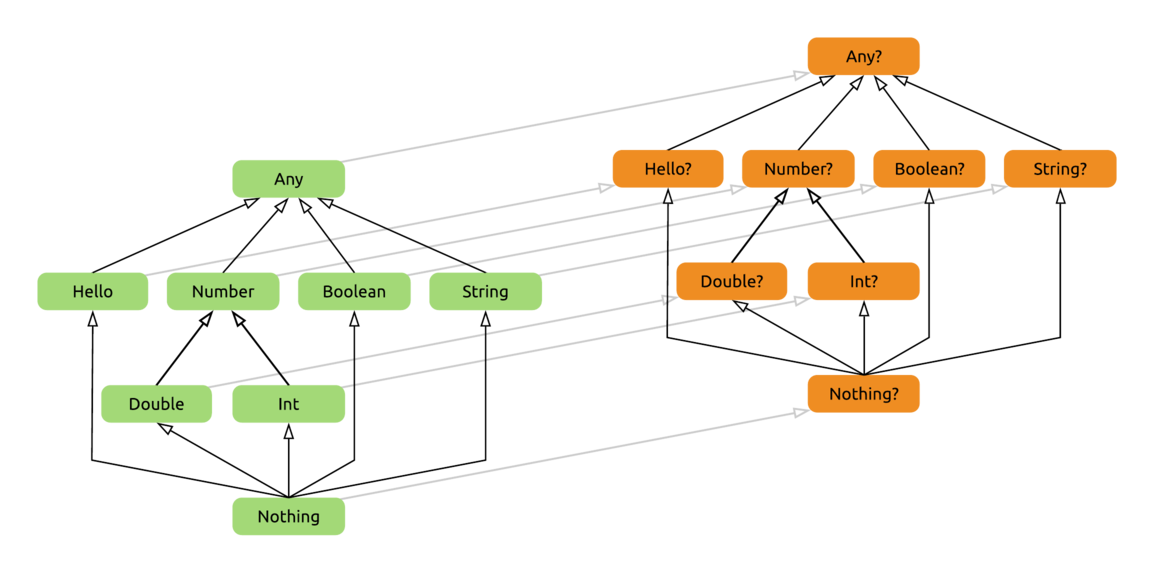
Why and how can Nothing serve this purpose? Think about for a second - anywhere you need a concrete type, be it an Int, a Dog, or an AbstractSingletonProxyFactoryBean, it’s safe to pass in something that has the type Nothing, because you know that this code can never actually be reached.

For example, the loopy function shown above will never return properly, which makes the variable assignment and then the call to this processData function safe in terms of type checking, albeit nonsensical:

fun processData(data: List<String>) {
    // Use data
}

fun main(args: Array<String>) {
    val data: Nothing = loopy()
    processData(data)
}

We see that the specific type of processData's parameter doesn’t matter. It could be any arbitrary type, and Nothing could still be passed in safely (as it will never actually be passed in).

Let’s move on to a use case where we can make more sensible use of Nothing being a bottom type.

Nothing and the Elvis operator

We’re going to bring two previous topics together now, Nothing and the Elvis operator.

Consider what happens when you use an Elvis operator with something of type Nothing on the right hand side. If the expression’s left side ends up being non-null, that’s the result of the expression, and we can continue on with our code. However, if we have to evaluate the “default” right side, execution of whatever function we’re in is guaranteed to be halted, as evaluating that side will either never terminate, or will terminate exceptionally.

I’m going to reuse the Nothing-returning exceptional function defined above for this example:

fun calculate(someParam: Int?) {
    val x = someParam ?: exceptional()
    val y = x * 2
    println(y)
}

Notice that we are using x as an Int on the second line where we’re multiplying it, and this code of course compiles and works correctly. This makes sense intuitively. If we were to run into the right hand side and call the exceptional function, calculate would not proceed due to the exception thrown from there, and otherwise we have a non-null Int on our hands.

However, let’s be precise and take a look at the type hierarchy again, and see what the return type of the Elvis expression should be:

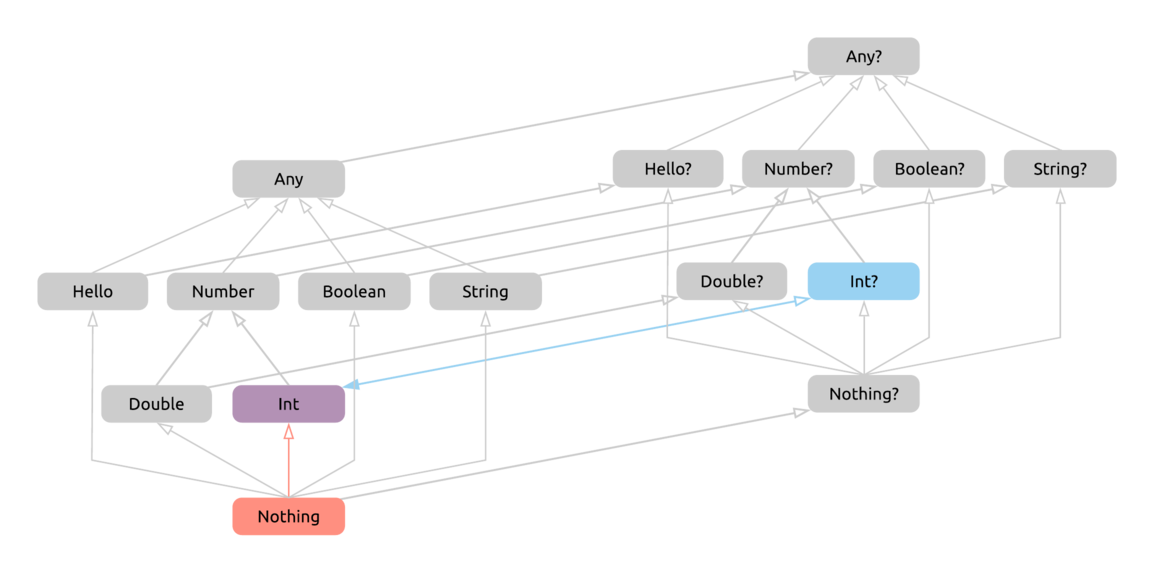
First, we take Int? back to the non-nullable hierarchy, and then we find the first common supertype of Int and Nothing, which, since Nothing is a bottom type, is Int itself! Notice that the same would happen for any nullable type on the left of the Elvis operator when there’s Nothing on its right side: the return type of the expression would just be the non-nullable variant of the type on the left.

This is already a quite nice way to handle null cases of certain values by throwing an exception, and have them be available on the next line conveniently as their original type, only its non-null variant.

We don’t even need to wrap throwing an exception into a function that returns Nothing. Like almost everything else, throw is actually an expression in Kotlin, and naturally, its type is Nothing. This lets us do simply this:

fun calculate(someParam: Int?) {
    val x = someParam ?: throw IllegalArgumentException("someParam must not be null")
    val y = x * 2
    println(y)
}

There’s another very handy little expression that can be used here for a different effect - the return expression. This lets us stop execution of this function for an invalid argument silently.

fun calculate(someParam: Int?) {
    val x = someParam ?: return
    val y = x * 2
    println(y)
}

Of course, we’re creating a new variable here that’s essentially the same as our parameter. This is both wasteful and somewhat confusing, especially in a longer function. Here’s a trick I’ve first seen somewhere on a Google I/O ‘17 slide:

fun calculate(someParam: Int?) {
    someParam ?: return
    val y = someParam * 2
    println(y)
}

Why does this still work? Because the Elvis expression (as every other expression) will be evaluated even when its value is unused, and if the parameter was null, we’ll return from the function. From the next line, someParam will be available as an Int due to a smart cast. (This of course can be used the same way with a throw.)

throw return

A weird quirk of both return and throw having a type of Nothing is that statements like this are perfectly valid in Kotlin:

fun oddity() {
    throw return return throw return
}

Why is this? Well, both return and throw take an argument that needs to be evaluated before they’re executed. throw takes a Throwable, and return takes whatever the return type of the given function is - in this case, it’s Unit, which is applied implicitly as a special case, but the same line would compile even if the function returned an Int and we ended it with return 82.

So, for the first throw to be executed, it needs a Throwable as an argument. The return expression right after it returns Nothing, which of course is a Throwable. Similiarly, whatever the function’s return type, writing either throw or return down after a return keyword will pass type checks, because Nothing will fit that return type.

Now we know why this compiles, but what happens when we run the code? The first expression needs its argument evaluated, which in turn needs its argument evaluated, and so on. At the end of this chain, only the very last expression will be executed, because whether it’s a throw or a return, it will exit the current function.

Now you know how to return values and throw expression in style.

About Nothing?

When introducing Nothing as a bottom type, we’ve updated our type hierarchy with two new types, but all we’ve discussed so far was the non-nullable Nothing. Does the nullable type make sense, and is it of any use to us?

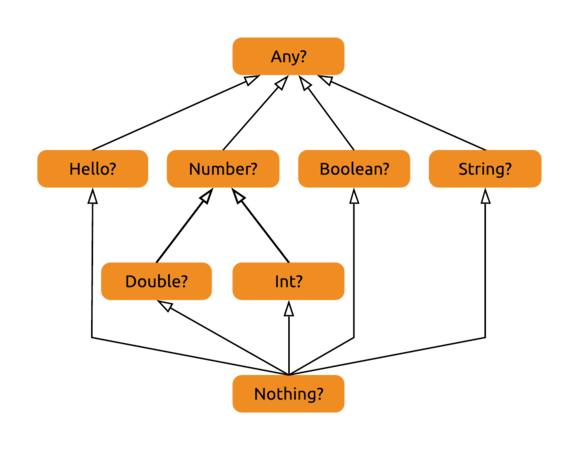
It’s a subtype of all nullable types, which would mean that a value of type Nothing? could be used anywhere where a nullable value is required. We know exactly one value that fits this description - null itself.

We can confirm our suspicion by assigning null to a variable, and letting type inference do its job:

val x = null

From here we can check with either reflection or again through the IDE’s tooling that x, in fact, is of the type Nothing? here. You almost never want to declare a variable like this, because you’ll never be able to assign it anything but null itself.

Here’s the common example of how people run into issues with this:

var x = null
x = "foo"

Although there’s a type that would work perfectly well here for both usages of x (the nullable String?), letting the compiler infer the type in this scenario leaves us with a scary-at-first error message:

Type mismatch. Required: Nothing? Found: String

Hopefully going forward this won’t scare you, and you’ll realize quickly that inference is to blame, and you can fix the issue with explicitly typing x as a String?.

Other recommended reading

For some other very clever and useful use cases of Nothing, I highly recommend checking out this and this article - if you made it this far, you’ll probably like them!

Conlusion

And that’s a wrap for now! I hope you’ve learned something new about the language, and can appreciate some of the very neat ways the type system is doing work for us. Don’t forget to apply the throw return idiom judiciously.